Fa un temps en aquest blog vaig escriure sobre el joc del caos i petites variacions. Aquests jocs es basen en el que a dia d'avui es coneix com el Teorema del Collage. Si llegim el que en diu la Wikipedia no s'entén pràcticament res (és el que passa amb molts teoremes).
Si mirem d'entendre què passava amb el joc del caos veiem que tenim 3 punts especials (cadascun dels vèrtex) i que estem fent una reducció de longitud des d'un punt qualsevol a un dels vèrtex. D'haver-hi només un dels vèrtex el punt cauria, inevitablement, cap al vèrtex: el vèrtex és un atractor. En ficar els 3 vèrtex junts el punt no acaba de caure mai en cap d'ells (tot i que s'hi acosta i es manté acotat) el que diu el teorema del collage és que l'atractor total és la unió dels atractors independents. Costa d'entendre però mirant una estoneta el triangle de Sierpinski un se'n fa una idea més o menys encertada.
El matemàtic Michael Barnsley al llibre fractals everywhere ens proposa un exemple combinant 4 transformacions afins (una mica més complicades que les del joc del caos). Esquemàticament tenen aquesta pinta:

La primera, representada en verd és una reducció d'escala de la coordenada y, amb una probabilitat de l'1% de ser aplicada:

La segona, representada per un rectangle blau s'aplica un 85% de les vegades:

La tercera, representada per un rectangle vermell s'aplica en un 7% de les vegades:

La quarta, representada per un rectangle blau fosc s'aplica en un 7%:
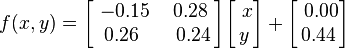
Si fem que l'ordinador ho dibuixi obtenim, efectivament, la falguera de Barnsley. A continuació veurem diferents figures amb 10, 50, 100, 500, 1000, 10000 i 50000 iteracions.







